Dear
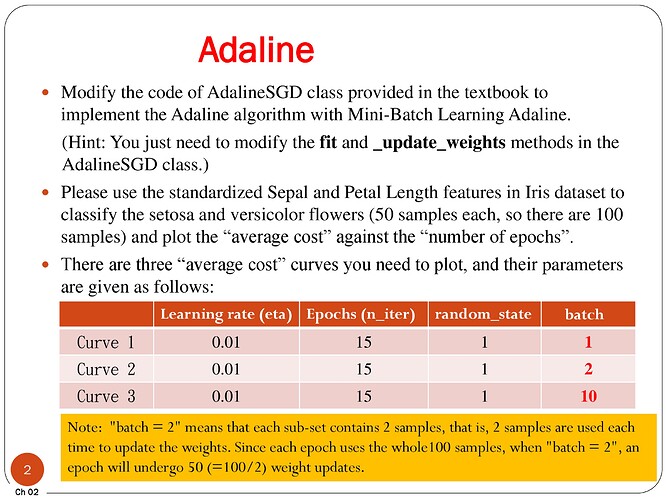
May I know how to modify my own Python programming so that I will get the
same picture as refer to the attached file - Adaline Stochastic gradient descent
(I am using the Anaconda Python 3.7)
Prayerfully
Tron Orino Yeong
tcynotebook@yahoo.com
0916643858
import numpy as np
class AdalineSGD(object):
def __init__(self, eta=0.01, epochs=15):
self.eta = eta
self.epochs = epochs
def train(self, X, y, reinitialize_weights=True):
"""Fit training data
X : Training vectors, X.shape : [#samples, #features]
y : Target values, y.shape : [#samples]
"""
if reinitialize_weights:
# weights
self.w_ = np.zeros(1 + X.shape[1])
# Cost function
self.cost_ = []
for i in range(self.epochs):
for xi, target in zip(X, y):
output = self.net_input(xi)
error = (target - output)
self.w_[1:] += self.eta * xi.dot(error)
self.w_[0] += self.eta * error
cost = ((y - self.activation(X))**2).sum() / 2.0
self.cost_.append(cost)
return self
def net_input(self, X):
"""Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
"""Compute linear activation"""
return self.net_input(X)
def predict(self, X):
"""Return class label after unit step"""
return np.where(self.activation(X) >= 0.0, 1, -1)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
X = df.iloc[0:100, [0, 2]].values
aln = AdalineSGD(eta=0.01, epochs=15, random_state=1)
aln.fit(X_std, y)
plt.plot(range(1, len(aln.cost_) + 1), aln.cost_ /100, marker='o', label='SGD1')
plt.plot(range(1, len(aln.cost_) + 1), aln.cost_ / 50, marker='x', label='SGD2')
plt.plot(range(1, len(aln.cost_) + 1), aln.cost_ / 10, marker='-', label='SGD3')
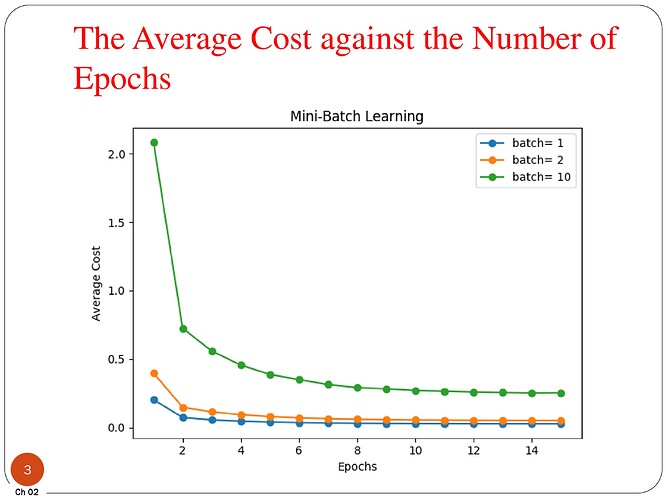
plt.xlabel('Epochs')
plt.ylabel('Average Cost')
plt.title('Mini-Batch Learning')
plt.show()