Strategic approach on how get same and different data with limited source in KNIME

KNIME Analytics Platform
22

Hi @trafalgarlaw , thank you for the updated information. Yes the rule governing the difference between UNIQUE and UNMATCHED was what I was looking for.

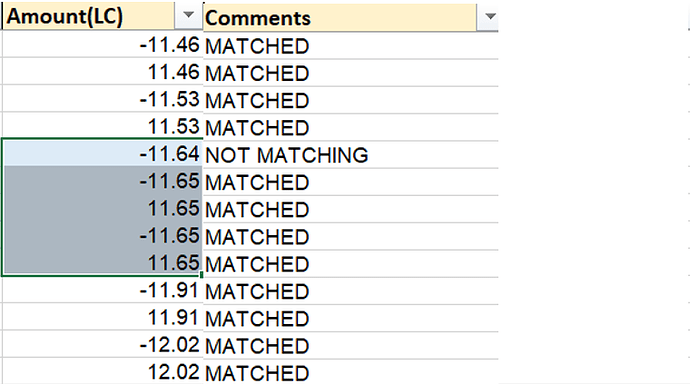
I would question the .03 difference being the cutoff because your previous examples have UNMATCHED pairs with a difference of .04 (2.0 and -2.04) and .05 (82.0 and -82.05) so with this new rule we can never achieve your previous expected results, but to my mind that is now just a threshold number that can be adjusted. The main thing is that it forms the basis for a rule.

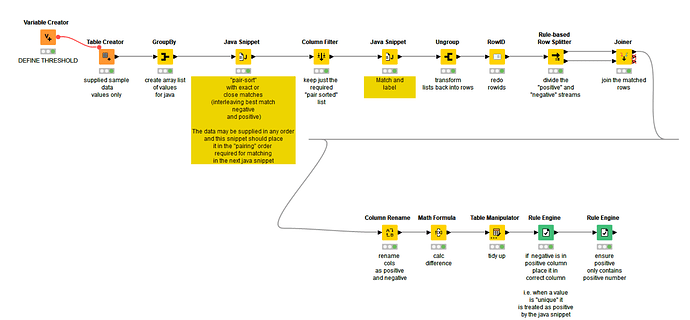
So, if I may now state what I believe to be your problem definition:

You have a list of numbers in no particular order.
Some may be positive and some may be negative.
Numbers may be repeated.
The members in this list need to be compared.

I’ll sometimes use the term “members” rather than “numbers” because it better signifies a specific instance of a given number in the list.

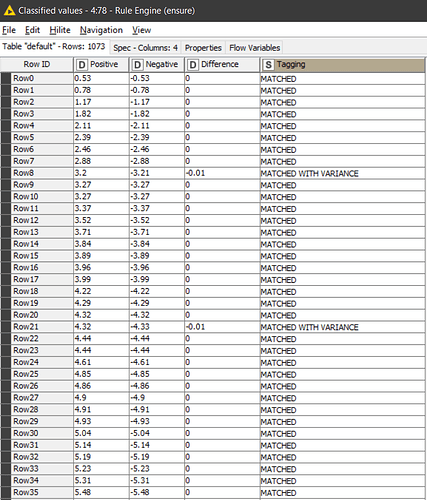
Where two members of the list sum to zero, the pair should be labeled “MATCHED” and take no further part in the comparisons.(edge case: it isn’t clear how to treat a pair of zeros. Are they special? I’ll assume they aren’t)

Of the remaining members if the difference between a pair of members is less than or equal to the threshold value (0.03), these will be labelled “UNMATCHED” and take no further part in the comparisons.

The members that remain are labeled “UNIQUE”.

No one member of the list of numbers may be considered matched or unmatched to more than one other member. Once it has been paired in this way it may not be paired with any other member. So the list 1, 2, -1, -1.01, -2, -2 would result in 1 and -1 being matched; thus -1.01 is unique, whilst one of the -2s would match the 2 leaving a lone unique -2.

What is potentially undefined is any order of precedence to unmatched values. Given the numbers 1.0, -1.01, -1.015 , 1.02 there could be two combinations of pairings since either positive could pair to either negative. The original post though would see these listed in ascending magnitude order 1.0, -1.01, -1.015, 1.02 and then pairings performed based on that ordering which would see the pairings 1.0 with -1.01 and then 1.02 with -1.015.

I think I can visualise how the above could be achieved, but I’m not currently at my pc. It would be good if you could confirm my understanding

1 Like
23

Hello @takbb, yes all your statement is correct. For zero amount, it is not included in the data, there will always a value like 0.01 or -0.01, plain 0.00 will not be part.

We can also reword ‘UNIQUE’ to ‘NOT MATCHING’ as I agree with your statement regarding the unique labelling.

For better representation, here’s the attached sample data with comments. You may filter the Comments by MATCHING, MATCHING WITH VARIANCE (MEANING UNMATCHED) and NOT MATCHING (UNIQUE OR NO PARTNER)

Amount Matching.xlsx (38.3 KB)

Hope this helps.

25

All of your data is in a single column. How do you determine which rows to compare in order to apply your matching rules?

26

Hi @trafalgarlaw ,

There were two challenges to this problem that on the face of it appear simple but had me scratching my head. The avenues I thought about using the core nodes became too convoluted, and still didn’t work. In the end, I had to fall back on java snippets and a lot more java code than I would normally want. In fairness, the beauty of KNIME is that even then, the code is less than if the whole thing were written in java.

I wrote it as two snippets.

One snippet ensured the sequence of numbers were presented in the order in which values could be compared for matching/not matched so although I used your sample data, the data could have been shuffled and it would still work.

The second snippet applied to rules to see if numbers matched.

The problem with using java snippets though is that they can only traverse forward through table data, never backwards, and certainly not “randomly”, so “sorting” and “sequencing” of the input data is not a normal use for them! However, there are some techniques that can be employed to get around this particular obstacle.

Instead of presenting the snippets with a table of multple rows, it gets provided with a table containing one row. But that one row contains all the data (i.e. in the form of an array list). :wink:

After the snippets have done their thing. The returned data (also returned as Lists) can be ungrouped to reform the required tables again, from which you can then get your results.

image
image1767×822 132 KB

I would prefer to have done it with less code, and if I think of a way, I’ll let you know, but I wouldn’t hold your breath!

Matched and Unmatched Pairings.knwf (67.5 KB)

image
image723×845 174 KB

If such a task is commonplace for you, then possibly parts of this workflow could be turned into components to make them a little more generic.

3 Likes
27

Thank you @takbb, always the best! I will try to review & try the workflow and let you know asap. :slight_smile: Really appreciate your greatness and for always sharing your expertise! Cheers!

1 Like
28

thats why it is complex my friend because the amount is in 1 column only hence seeking help here. anyhow, will check takbb’s workflow and will let you know too if works for all our samples. thanks for your ideas as well

29

It worked @takbb, thank you so much! But will try to review the java coding hope I can decipher :sweat_smile: but yeah will look forward to your advise if there will be a general one that me as a beginner to grasp the workflow fully. :slight_smile: Again, really appreciate your time and effort. Always grateful!

1 Like
30

Hello @takbb, we’ve tried for other sample data but I’ve noticed a slight difference.

Here are some samples:

This is the actual data:

image
image760×424 78.2 KB

This is the KNIME result:

pairSortedList NumberStatus
-11.64 MATCHED WITH VARIANCE
11.65 MATCHED WITH VARIANCE
-11.65 MATCHED
11.65 MATCHED
-11.65 NOT MATCHING

I think this is also my mistake that I did not consider or state this kind of scenario that may happen.

With this, the correct way for matching is the 11.64 should be tagged as NOT MATCHING (UNIQUE OR NO PARTNER) then the rest 11.65 should be MATCHED. I am not sure if this can still be considered in the scripting or not because it seemed hard to remediate per my perspective but let me know if you have any ideas.

Apologies and thank you so much, @takbb!

31

Apologies, here are other numbers and here’s how they are arranged and it just that 11.64 was paired to 11.65 but 11.64 should be tagged as ‘NOT MATCHING’ (UNIQUE or No Partner)

11.28
-11.29
11.28
-11.29
-11.41
11.41
-11.46
11.46
-11.53
11.53
-11.64
11.65
-11.65
11.65
-11.65
-11.91
11.91
-12.02
12.02
12.02
-12.02
-12.02
12.02
-12.36
12.36

32

Hi @trafalgarlaw , thanks for the info. It looks like a revisit to the algorithm that sequences the rows initially is going to be needed.

I’ll take a look when I get a chance. Hopefully later today.

33

Thank you, @takbb! Apologies for a follow up questions after your solid solution :slight_smile:

34

Hi @trafalgarlaw , try this one
Matched and Unmatched Pairings - 2.knwf (79.1 KB)

I had to change the way the first java snippet derives the sequence of the rows, so it now does 2 passes. The first pass tries to match all “exact opposites” (i.e. threshold = 0), and only then does it try to pair remaining rows which are within threshold. That should then mean the second snippet can process as per your latest data set.

I have done a cursory check that the original data set still works correctly, but you will need to test this for yourself of course.

3 Likes
35

Thank you, @takbb. I will check and let you know asap for the results. :slight_smile: