Decision Tree / Random Forest - Study purposes

[Felipereis50]

Hi friends

I would like to talk about “Random Forest” and “Decision Tree.”
This post is purely for study purposes.

Let’s go!
I have watched several videos on this topic, many of them from Knime itself.
Recently, I watched a video by Scott Fischer, which was quite entertaining, by the way.

In Knime’s examples, there’s one related to diseases where age and body fat percentage are compared with heart disease.

In these examples, I noticed that several variables (columns) lead to two distinct outcomes.
For example:

Age + Body Fat + Family History + etc. + etc. = Heart Disease YES
Age + Body Fat + Family History + etc. + etc. = Heart Disease NO

But since we select a “target column,” could I simulate the calculated value of a mathematical formula?

For this reason, I thought of conducting a practical test related to my field of work.
This test is just a simple mathematical calculation that results in an expected value based on a mathematical formula for all columns.

Let’s look at an example:

I thought—if I create a mathematical calculation with a logical rule, only changing the values of quantity and unit price, but define a column as a string to categorize the obtained result—could I identify which columns are “YES” and which columns are “NO” without having a calculated column defining the result?

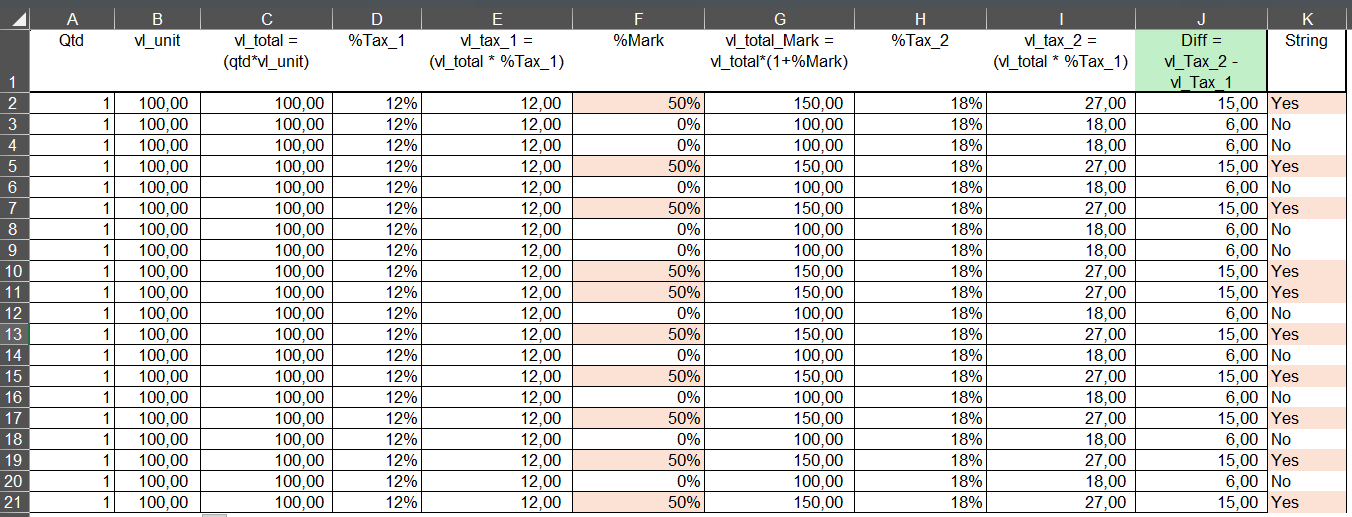
Analyzing the Table:

Data base 1

Check print 1: a table with a mathematical calculation.

• Column 10 represents the last step of the mathematical calculation.
• Column 11 is a string column that checks whether the value in column 6 (50%) is greater than zero.
  • If greater than zero → YES
  • Else → NO

Notice that the value in column 10 is always higher when there is 50% in the calculation.

With this, I started the Random Forest model, considering all columns.

---

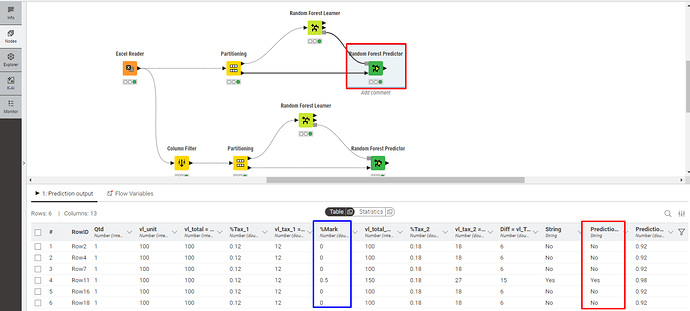
Test 1 - All Columns

In this test, the predictor node correctly classified all cases.

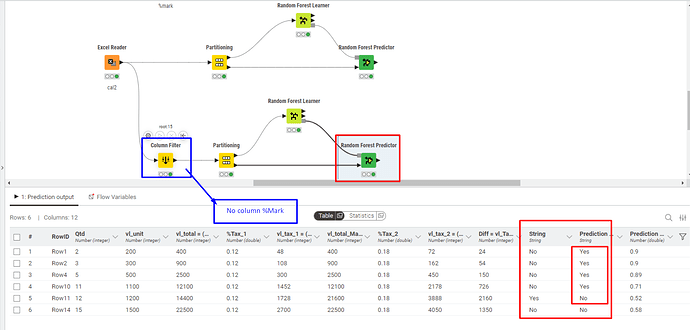
Test 2 - Without Column %Mark

In this test, the predictor node also correctly classified all cases.

If I stop here, it is clear that the Random Forest correctly predicted the final outcome, considering the columns.
I envisioned this scenario assuming that, in a new dataset, I would not have the %Mark column in my data.
Then I thought—could I still predict the outcome using only the remaining results?
So far, yes.

---

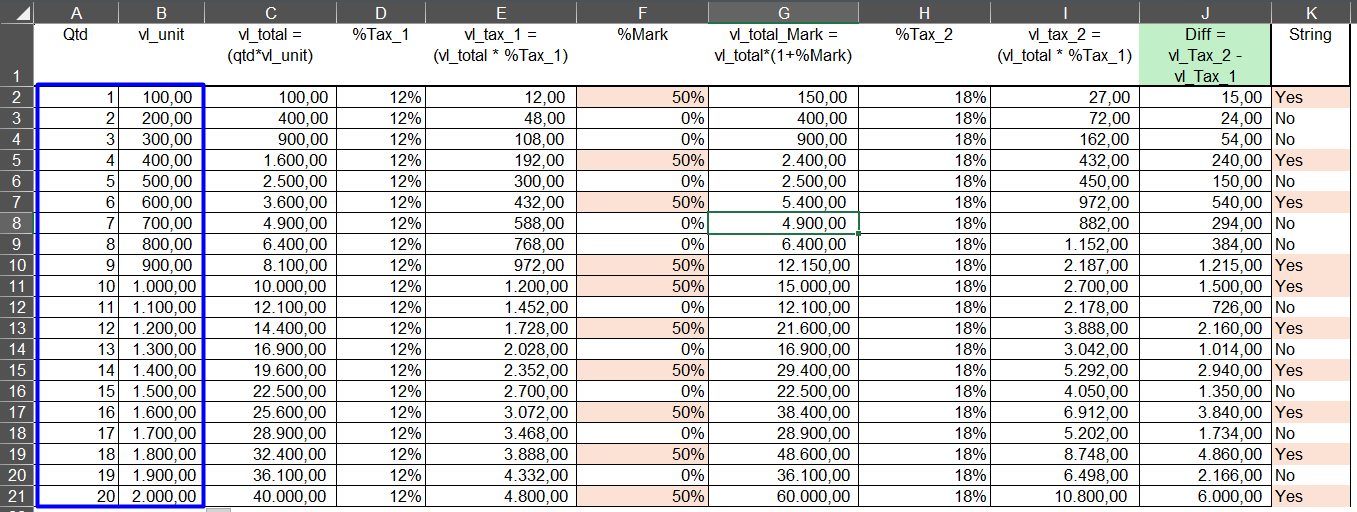
Now, let’s continue with another test, but this time altering the quantity and unit price of the items while keeping the same mathematical formula.

I created another file and modified the quantity and unit price for each item, making the dataset less standardized compared to the first case.

Notice that the final values are quite different, but mathematically they make sense.

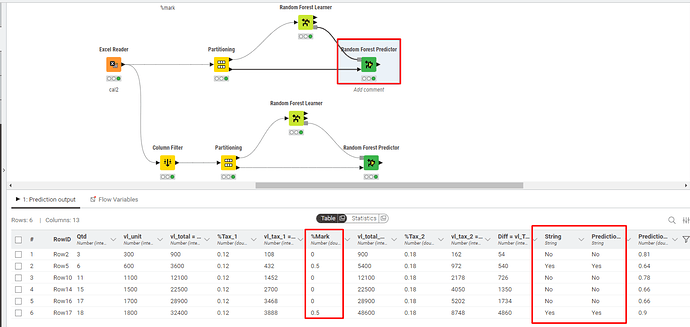
Test 1 - Keeping the %Mark Column

Random Forest correctly classified all cases, even with a less standardized dataset.

Test 2 - Excluding the %Mark Column

Random Forest did NOT correctly predict the final outcome.

In this case, I believe that since the dataset became less standardized and no longer contained a key column for comparison with the string (target) column, this might have been the reason for the incorrect predictions.

---

Summary:

Perhaps I need more rows in the partitioning step.
PS: I’m using 70% > 30%.

Teste-Decision Tree.knwf (122.5 KB)

Question: I would like to know why, in the last case, the result was not as satisfactory.

[k10shetty1]

Hi @Felipereis50,

Thanks for sharing the detailed tables.

From what I see, most of your features — like vl_total, vl_tax_1, vl_tax_2, vl_total_Mark, and Diff — are mathematically derived from just a few core inputs: Qtd, vl_unit, and %Mark.

So when you remove %Mark, you’re not just dropping one variable — you’re removing a key input that feeds into multiple other fields. Since those derived fields don’t add new information (they just restate existing data), the model loses predictive power.

To improve generalization, consider creating features that aren’t simple formulas, such as:

• Binning Qtd into categories (e.g., bulk vs. retail)
• Flags for high markup (%Mark > 25%)

These can offer the model more independent signals and lead to better performance.

Best,
Keerthan

[Felipereis50]

Hi friend.

Thank you…

I’d like to ask another question.
Do Random Forest or Decision Tree models get better each time they are used with a dataset?

What I mean is: when I generate the first dataset with Random Forest/Decision Tree and get a result of 70%, if I use the same model (PML) on a new, updated dataset, will the result become more accurate over time? Or not — is it just the initial learning that matters, and using it multiple times won’t necessarily lead to 99% accuracy?

So, in that sense, a Decision Tree isn’t like an AI that keeps improving and learning from the data.

I’m not sure if I was clear with my question.

[rfeigel]

Random Forests and Decision Trees have learned all they’ll ever learn from the original training data. There are a variety of techniques which can be employed which may improve the results, but these approaches are deterministic. Once a model is trained it won’t do more on its own.

[Felipereis50]

Thanks for the explanation.