Find combination of columns summing to specific value

KNIME Analytics Platform
8

Hi @shubh,

I’m inclined to agree that this problem is probably best solved using a python node, based on the logic that you supplied. However, a challenge is a challenge… :slight_smile:

So, having decided that I couldn’t find any “quick wins” using nodes designed specifically for this type of task, I considered how to firstly derive the combinations. That is actually relatively easy, since you have a set of data columns and each is to either be included or excluded from each iteration, so its a binary decision. The total combinations from n columns is therefore “(2 raised to the power of n) minus 1”. Minus 1 because we exclude where no columns are involved. We assume we always want to include at least one column.

So there is at least one loop required here (the number of combinations), and as you increase the number of columns, you keep doubling the combinations and so this process will quickly become horribly slow, but assuming you have powerful tech, or plenty of time, here goes… :wink:

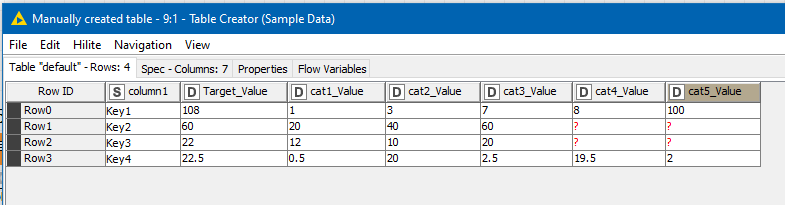
image
image1411×484 38.7 KB

The sample data I used was this:

image
image785×205 8.84 KB

The first few nodes prior to the loop simply count the column names of the form “catn_Value” and determines the number of iterations required to achieve the combinations. In the case of the sample table, there are 5 data columns, and therefore there will be 2^5 - 1 = 31 iterations.

For each iteration, an output column name is derived, which will be OutTotaln where n is between 1 and in this case 31.

The fun part in all this is the Column Expression node. This contains a further loop of its own, as it must loop through each of the columns.

For each combination (1 to 31), it must determine which columns (1 to 5) should be included. It uses the binary version of the iteration to do this, treating each column number (1 to 5) as if it were a “bit” .
The binary representations of 1 to 31 are:

1  = 00001
2  = 00010
3  = 00011
4  = 00100
...
...
28 = 11100
29 = 11101
30 = 11110 
31 = 11111

and this is useful as it tells us the combination of columns to include for each iteration. “1”=include, “0”=exclude.

The Column Expressions node is basically javascript, and (because I’m lazy!) I got a quick javascript snippet which determines whether the kth bit is set in a given number from here:

This node loops through each of the “value columns” and if, for that column number (1-5), the bit is set for the current combination-iteration (1-31), it adds the value of that column to a running total. If at the end, the total is the same as the target value column in the data table, it returns the values for that combination of columns. If it doesn’t it discards it.

n=variable("currentIteration")+1
s=""
tot=0
delim=""
for(colno=1; colno<=variable("Number Columns");colno++)
{

    if (not(isMissing(column("cat"+colno+"_Value"))))
    {
        if ((n & (1 << (colno - 1))) > 0)
        // if the bit represented by colno  is set in the current iteration n, then include
        // the value of the colno column in the total
        {
            tot=tot+column("cat"+colno+"_Value");
            s=s+delim+column("cat"+colno+"_Value");
            delim="+"
        }
    }
}
if (tot==column("Target_Value"))
{s}
else
{""}

This is then performed in the loop for each combination.

At the end, we have a series of columns representing the result for each iteration. This is then aggregated to keep just those where an actual (no empty) result was returned, and it is appended back onto the original data set.

image
image1318×186 11.4 KB

Column Combinations.knwf (37.2 KB)

2 Likes