Adding two numbers deviates from expected result

[mwiegand]

Hi,

I created a workflow to calculate the Fibonacci sequence with the purpose to:

1. Use the process to scale up test workflows i.e. for performance testing or bug hunting
2. Publish a series of articles
3. Show and provide education for Knime Starters (one challenge, many solutions)
4. Educate and challenge myself to understand mathematical principles and how to transform them into some sort of “analogue” representation

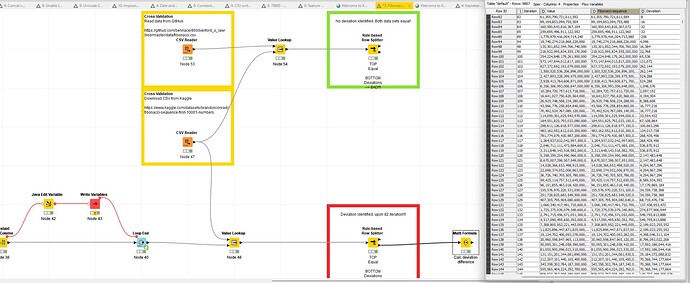
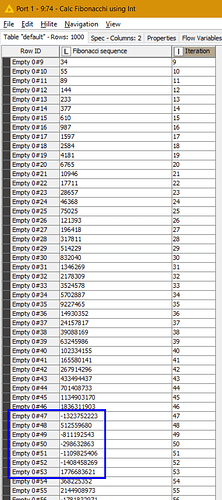
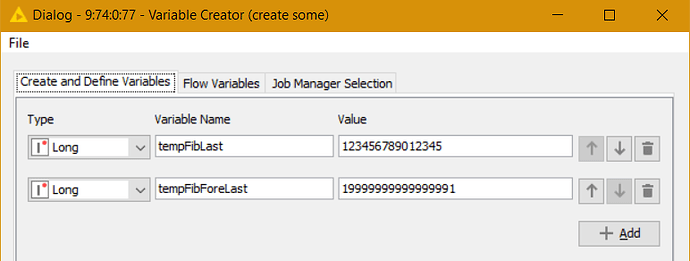
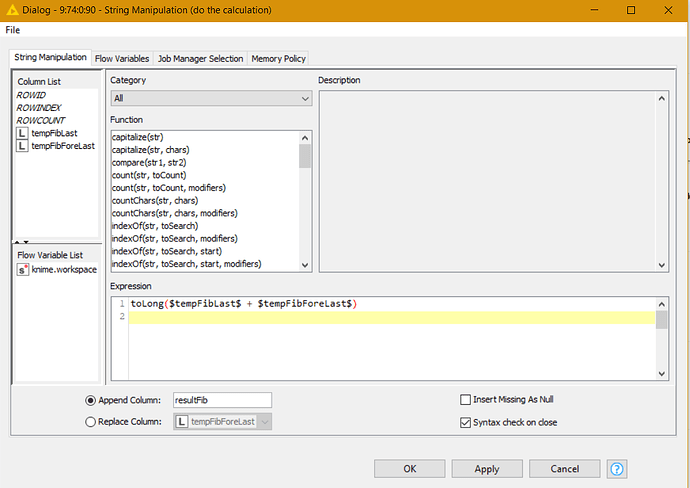
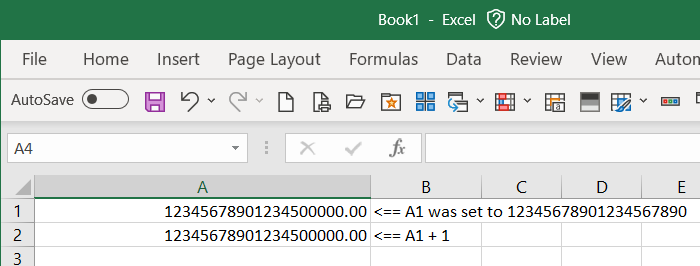
The logic is simple, if the initial results equal to the expectation, the solution is correct. The problem I noticed, when calculating the Fibonacci sequence and cross verifying it with two independent resources (Kaggle & GitHub), there is a deviation upon the 82 iteration.

Most interestingly, the deviation starts with -8 and keeps increasing by that factor which makes me wonder, given the are eight bits in a byte, if there is a connection.

On another occasion, albeit being a more complex mathematical scenario, I happen to notice a deviation as well. Though, that really might be a mistake on the workflow.

Calculate Kaprekar-Konstante/Routine: Where is my mistake?

Hi all, I am uncertain if this rather mathematical question belongs here so please allow me to explain it first. In an effort to evaluate a system performance to find / suggest ideal settings for Knime (memory utilization, parallelization etc.), I had the idea to use reproducible mathematical solutions. One example which caught my interest today, that can be rather CPU straining, is calculating the Keprekar Constant / Routine (Wikipedia english / german). However, after computing the resul…

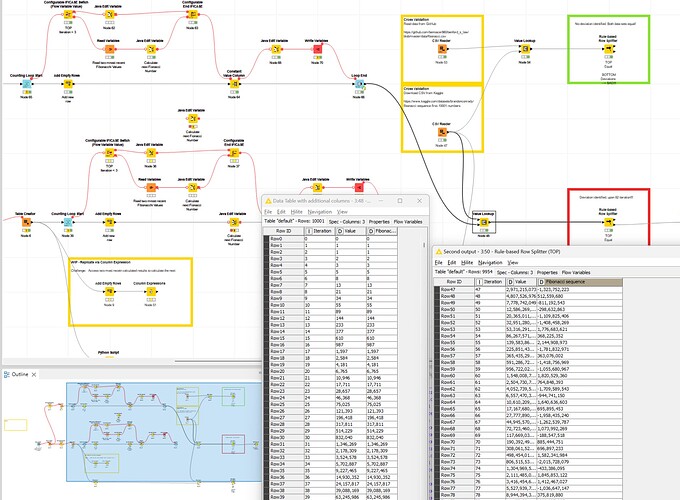
I hope I am the problem here and not Knime Here is the test workflow:

Fibonacci Sequence – mwiegand

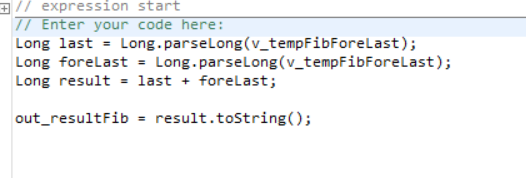
PS: I replicated the exact same issue, failing at the 82nd iteration, even through other means using Python too which points towards a more fundamental issue. The test workflow was updated with the latest changes.

Best
Mike

[nan]

My first guess would be that this is a precision limitation of the Double floating point data type/addition. Did you try using Long numbers?

Cheers,
nan

[mwiegand]

Good guess. I switched to double as the workflow failed with long. I will try that again. Going to report back once I got an update.

Update: @nan switching to int makes the issue even worse. It works until the 46th iteration but then breaks apart entirely.

I uploaded a new test workflow:

79123 - Adding two numbers deviates from expected result - Fibonacchi Series...

[takbb]

Hi @mwiegand , I think the issue is indeed one of precision.

Unfortunately the precision of a java Double data type is notoriously poor, when we get to large values.

So… as per the previous suggestion, you have attempted to use Long, but…

Unfortunately, KNIME’s support for Long is very poor!

• its presence breaks the String Manipulation (multi) node
• String Manipulation (Variable) cannot see Long variables
• Math Formula (Variable) cannot see Long Variables
• Variable Expressions cannot see them or create them
• Java Edit Variable cannot read or create Long variables. It can only create Integer variables.

… the list probably goes on!

The last point I think is what is “breaking” the int version of your code.

Such issues have caused me to wonder exactly what data type we should be using for large values, as KNIME has no numeric datatypes that can handle large values with good precision across its nodes.

Back to your specific issue with the “int” version… If you look at the output for your Int metanode, you can see that it begins to switch between negative and positive results, which is a sure sign the value has gone “round the clock” and busted the Integer range limit.

So what to do?

While doing a bit of research here, I found that to get a java edit variable to sucessfully perform your required Long calculations would involve using a whole succession of nodes such as this example:

Basically, you need to convert (marshal) the Long variables to Strings and within Java Edit Variable you would have code such as this, to calculate the result of these as Longs, and then output this again as a String, e.g.

But then another thought occurred to me, that if we need to do all of this using String Manipulation (ironically, one of the very few nodes that can actually handle Longs!), then why not just use String Manipulation for the job of calculating:

e.g. given two Long variables:

The result of the sum of two Longs can be calculated by String Manipulation (edit: after they have been converted into columns!) as follows:

I haven’t tried plugging such functionality into your workflow, but I suspect that if it could be incorporated in place of the Java Edit variables, you would get closer to the result that you are looking for.

Better support for Longs is long overdue in KNIME though, and if I could change just one thing about KNIME it would be this!

[mwiegand]

Hi @takbb,

this is interesting and frightening to read at the same time considering that Knime is meant, and I am afraid to speak that out loud given the context, considered to work with large data sets / big data.

An overflow error for an int, ok, can happen. Though, 100 million digits is safe to assume works for most people. But for long supporting a length of 15 digits not to mention a double with 1023

Type	Size (bits)	Minimum	Maximum	Example
byte	8	-2^7	2^7– 1	byte b = 100;
short	16	-2^15	2^15– 1	short s = 30_000;
int	32	-2^31	2^31– 1	int i = 100_000_000;
long	64	-2^63	2^63– 1	long l = 100_000_000_000_000;
float	32	-2^-149	(2-2^-23)·2^127	float f = 1.456f;
double	64	-2^-1074	(2-2^-52)·2^1023	double f = 1.456789012345678;
char	16	0	2^16– 1	char c = ‘c’;
boolean	1	–	–	boolean b = true;

A little anecdote … .ever heard of the issue with Xerox scanners not scanning correctly. That issue basically rendered all documents - legal, tax, insurance, you name it - obsolete.

Just imagine the impact a similar issue could have but in a much more connected world. I personally don’t want to overreact but, and I absolutely agree with your conclusion @takbb, that this requires immediate attention. Especially since it lingers around for some time.

Xerox scanners/photocopiers randomly alter numbers in scanned documents

Thinking this a bit further, extracting the row index, which I personally prefer over row ids, and trying to merge data but data ends up in the wrong place. Or when thinking about genetics and one might split each base of a genome into rows (just an arbitrary example). Or much simpler, financial analysis, cryptography, power grid statistics …

I wonder how others see the criticality of this.

Best
Mike

[takbb]

@mwiegand

this requires immediate attention.

following on from your xerox anecdote… my response is

Copy That!

btw It should be noted that whilst 64-bit double values can take values in the range to 2^1023, they are not accurate to anything like that, and only have precision to 15-17 digits

[mwiegand]

Touché About the precision, I would have never thought, if a supported range is given, that within that inaccuracies can occur. That put the recent findings of 100 trillion digits into a different perspective. Certainly they didn’t use Java …

[takbb]

lol, mind you it’s not just java. It’s the limitations of what can be held within 64bits. There has to be approximations when you consider that there are actually an infinite number of numbers (if we are talking non-integers) between any two numbers, and that’s before we get started on rounding issues with calculating in binary vs representation in decimal.

But to see this kind of “signficant digit rounding” in action, you just need to open Excel.

Into cell A1 type the number 12345678901234567890
Set the format for the cell to “number” so that you can see all the digits. You will see it has already lost precision to the first 15 digits.

In cell A2, type =A1+1

Cell A2 will now be the same value as cell A1, because it cannot hold that level of accuracy

[mwiegand]

Good morning @takbb,

I was resuming work about aa test workflow for the community hacking days and for knowledge sharing. While further educating myself I found this very nice article from @DiaAzul which also might be of interest for you too:

High-Precision Calculation Using KNIME

Best
Mike