Update to v1.22.0 - New PMI Nodes

[Vernalis]

We have just released another update to the nightly build.

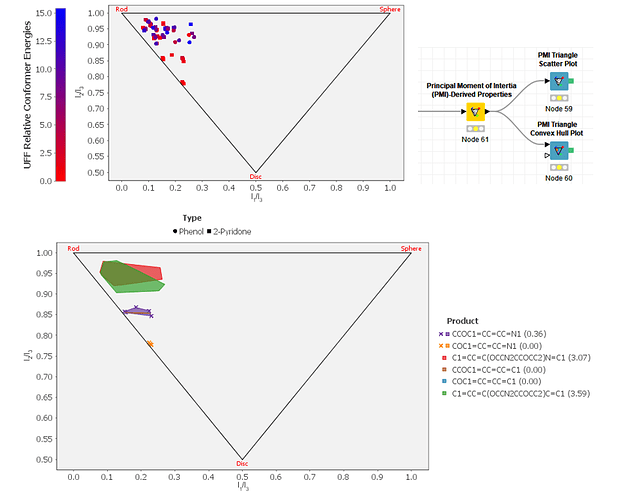
In this latest update, we have retired the existing PMI Calculation node which has been in the public domain since v1.6.4 (April 2016), and replaced it with a new node Principal Moment of Intertia (PMI)-Derived Properties. This uses a new underlying framework, and is no longer dependant on RDKit. It also now accepts CTab and PDB cells as inputs. The new framework also sets column properties with a brief description, units, literature references, aliases and minimum and maximum values where available. The node also calculates many more PMI-related properties (20 in total). The properties are:

• PMI 1 - First (smallest) Principal Moment of Inertia (also referred to as: I₁)
• PMI 2 - Second Principal Moment of Inertia (also referred to as: I₂)
• PMI 3 - Third (largest) Principal Moment of Inertia (also referred to as: I₃)
• npr1 - First Normalised PMI (i.e. I₁ / I₃) (See: Sauer and Schwartz, J. Chem. Inf. Comput. Sci., 2003, 43, 987-1003)
• npr2 - Second Normalised PMI (i.e. I₂ / I₃) (See: Sauer and Schwartz, J. Chem. Inf. Comput. Sci., 2003, 43, 987-1003)
• Sigma npr - npr1 + npr2 (also referred to as: Flatsum, npr1+npr2, Σnpr) (See: )
• Sphericity - npr1 + npr2 - 1 (also referred to as: S) (See: Wirth et al., J. Comput. Aided Mol. Des., 2013, 27, 511-524)
• Rodlikeness - npr2 - npr1 (also referred to as: R, Rod-likeness) (See: Wirth et al., J. Comput. Aided Mol. Des., 2013, 27, 511-524)
• Disklikeness - 2 - 2 × npr2 (also referred to as: D, Disc-likeness) (See: Wirth et al., J. Comput. Aided Mol. Des., 2013, 27, 511-524)
• Asphericity - 0.5 × [(I₁ - I₂)² + (I₁ - I₃)² + (I₂ - I₃)²]/[I₁² + I₂² + I₃²]; 0 corresponds to a spherical top and 1 to a linear molecule. ~0.25 corresponds to prolate (cigar-shaped) molecules, and disc-shaped ~1 (also referred to as: ΩA) (See: Arteca, Reviews in Computational Chemistry, Vol 9 VCH, NY, 1991, 191-253)
• Inertial Shape Factor - I₂ / (I₁ × I₃); Undefined for planar molecules (also referred to as: S_I) (See: Lister et al., Internal Rotation and Inversion, Academic Press, London, 1978)
• Molecule Eccentricity - √(I₁² - I₃²) / I₂; 0 corresponds to a spherical top, and 1 to a linear molecule (also referred to as: ε) (See: Arteca, Reviews in Computational Chemistry, Vol 9 VCH, NY, 1991, 191-253)
• Gyradius - Radius of Gyration (also referred to as: RG, Radius of Gyration, Gyradius) (See: )
• Gyradius 2D - Radius of Gyration (2D) = √(I₁ × I₂) / MWt (also referred to as: RG, Radius of Gyration, Gyradius) (See: Volkenstein ‘Configurational Statistics of Polymeric chains’ Wiley, NY, 1963)
• Gyradius 3D - Radius of Gyration (3D) = ∛(I₁ × I₂ × I₃) / MWt (also referred to as: RG, Radius of Gyration, Gyradius) (See: Tanford ‘Physical Chemistry of Macromolecules’, Wiley, NY, 1961)
• PRG 0 - 1st Principle Radius of Gyration (R0 = √(I₁ / MWt)) (also referred to as: R0) (See: Jian et al., ‘A dimension map for molecular aggregates’, J. Mol. Graphics. Model., 2015, 58, 10-15)
• PRG 1 - 2nd Principle Radius of Gyration (R1 = √(I₂ / MWt)) (also referred to as: R1) (See: Jian et al., ‘A dimension map for molecular aggregates’, J. Mol. Graphics. Model., 2015, 58, 10-15)
• PRG 2 - 3rd Principle Radius of Gyration (R2 = √(I₃ / MWt)) (also referred to as: R2) (See: Jian et al., ‘A dimension map for molecular aggregates’, J. Mol. Graphics. Model., 2015, 58, 10-15)
• Gyradius Ratio 1 - 1st Gyradius Ratio (r1 = PRG1 / PRG0) (also referred to as: r1) (See: Jian et al., ‘A dimension map for molecular aggregates’, J. Mol. Graphics. Model., 2015, 58, 10-15)
• Gyradius Ratio 2 - 2nd Gyradius Ratio (r2 = PRG2 / PRG0) (also referred to as: r2) (See: Jian et al., ‘A dimension map for molecular aggregates’, J. Mol. Graphics. Model., 2015, 58, 10-15)

We have also added the first two of a family of PMI Plotting nodes, based on the JFreeChart integration withing KNIME. These first two nodes provide a standard PMI Scatter plot, and a Convex Hull PMI Plot (which can have an optional scatter point set overlaid onto it):

There will be more releases with further new nodes in the coming days.

Yours,

Steve

[Kovaid]

Hello,

I am not sure if it is the right place to write, if it is not then please direct me in the right direction.
So my issues is, I have tried to use the PMI plot but I only get all my data points on the rod-disk axis.
My workflow looks like: SDF reader -> PMI derived properties -> PMI triangle scatter plot.
In the PMI calculator I just calculate the npr1 and npr2 and then trying to plot it with the PMI plotter.
I do not know what can be the issue or I do not know what I am missing.

Thanks for the help.

Best regards,
Dan

[Vernalis]

Hi Dan,

Yes, this is definitely the right place to post. The most common cause of this is that your molecules don’t have 3D co-ordinates, in which case they will all be ‘flat’, and so on the Rod-Disk axis. The easiest way to tell is if you look at the structures in the output of your SDF reader node - if they look nicely laid out but not showing 3D conformations, then you almost certainly have 2D coordinates, in which case you need to add them first using one of:

Templated Conformer Generation (RDKit)

(You don’t need a template for this node but you can have one if that is relevant!)

RDKit Add Conformers

RDKit Generate Coords

(All three of the above use RDKit but offer some different options depending on what degree of control you want)

3D Coordinates

Generate 2D Coordinates

Steve

[Kovaid]

Hello Steve,

Thank you very much for the help.
It actually worked.

Best,
Dan