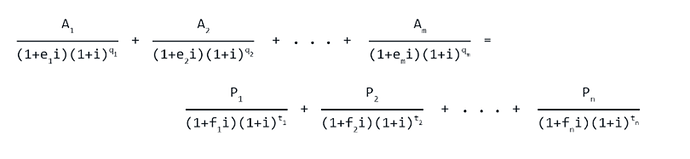XIRR unexpected results

[mikdnjneer]

First off, thank you Christian Rastasanu and Paolo Tamagnini (@paolotamag and whoever else involved) in the creation of the Financial Calculation verified components and its training materials.

Use Case:
I have a set of “scenarios” for which I have cash flow records I generated myself as a control group for testing of my workflow. Therefore, I know the interest rate I used to generate them, along with other important factors such as compounding period.

Example Scenario:

• $100k investment/60 equal monthly payments in arrears/interest rate of 8%
• Day count convention is 30/360 – leading to 12 compounding periods a year.
• Resulting payment amount is $2027.64 due the same day of the month, every month.

Issue:
I have tried the XIRR node. The speed is amazing. My baseline group using “Parameter Optimization Nodes” took 3 minutes, and my baseline group using XIRR was done in less than 5 seconds. However, I am unable to produce the same results. I get 8.3% IRR (instead of 8%). I am not able to recreate this result through other calculation methods.

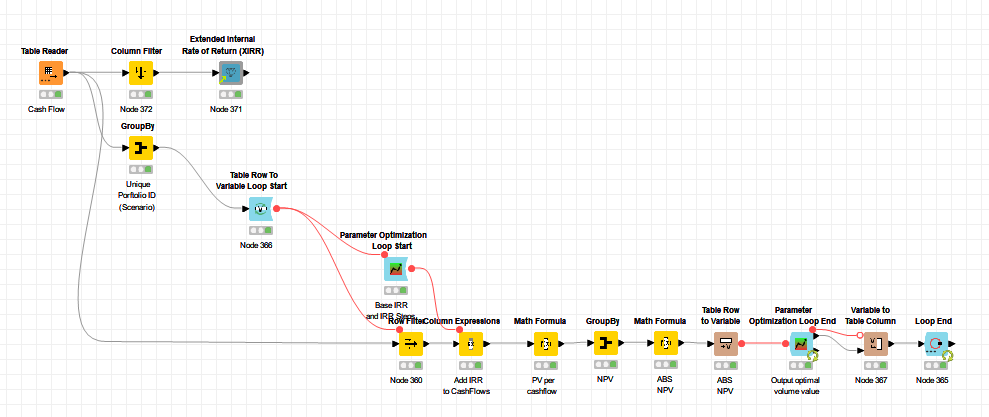
I have tried to research the calculation in the “Java Snippet – XIRR(de campo)”. However I am not a developer and I don’t understand java or how to navigate it in GitHub. Can someone help me either speed up my “Parameter Optimization” loop, or understand why the XIRR is not producing my desired results?

Desired IRR method
I am calculating the IRR in accordance with “Appendix J” of the “Truth in Lending Act”. It is your standard textbook IRR formula which considers compound periods, and partial periods as well. At the moment I am only interest in monthly compounding, but will soon neither other frequencies.

I have used the goal seek function of excel to validate the reverse calculation (meaning, I have used the cash flows and their characteristics such as compounding period with the formula mentioned above to solve for IRR), and have achieved the desired results.

I have used Ivory’s “Supertrump” (an industry leader in pricing applications for equipment finance), and validated the results as well.

I have recreated the goal seek function of excel in KNIME using “Parameter Optimization Nodes”. Here I also get the desired results. My challenge here is the speed. I have 100k scenarios, each with up to 120 cash flows for which I want to solve IRR. Right now it is taking me about 30 seconds per scenario.

My desired outcome would be able to pass additional cash flow parameters (see appendix J, section 8) into an XIRR like node and obtain the IRR with the same speed as the XIRR node does now. The node would have defaults to choose from if certain parameters were not supplied. With recent federal and state regulations requiring more and more companies to adhere to the “Truth in Lending Act”, this would become a very popular node.

KNIME_IRR.knwf (414.7 KB)

IRR.xlsx (27.8 KB)

For reference:
NPV Formula for which to solve IRR
Appendix J - NPV Formula Definition

Parameter Optimization Loop:
KNIME - Parameter Optimization Loop

Financial Calculations in KNIME:

Automating Financial Calculations with KNIME Webinar

Attention all financial analysts! In the field of financial investments, making informed decisions is crucial. Furthermore, the traditional Excel calculations for metrics like NPV and IRR can be time-consuming, tedious, and complex, especially when dealing with multiple projects. Discover the game-changing power of dedicated financial components in #KNIME Analytics Platform. Say goodbye to manual calculations and hello t…

[mikdnjneer]

Updated the KNIME workflow attachment to include the data.
Sorry about that.

KNIME_IRR-updated.knwf (185.0 KB)

[ScottF]

Tagging @crastasanu for completeness

[Residentstiefel]

Hi @ScottF & @crastasanu,

Any updates on the issue?

I digged into the workflow and couldn’t find any hint that yields to a different result. Also, I tried to find something in the documentation, as my initial gut feeling was that the results are due to a different day count convention. But the documentation actually suggests 365 day convention. Also, I checked if the leap year in 2028 could be the problem, but negative.

This is a crucial KNIME component for the financial industries, so I think it is quite urgent to get to the roots of it

Cheers,
Stiefel

[paolotamag]

Hello everyone,
Great to see you are using these verified components for finance analytics.

I cannot at the moment get into the details on why your method returns different results,
but I can shed some light on how we built and verified the components.

First of all there in total 4 components:

• Net Present Value (NPV)
• Extended Net Present Value (XNPV)
• Modified Internal Rate of Return (MIRR)
• Internal Rate of Return (IRR)
• Extended Internal Rate of Return (XIRR)

Examples for all components can be found here:

mydral/Finance Metrics - Verified Components Examples

A webinar where @ presents the components can be found here:

Automating Financial Calculations with KNIME

In each case we computed the scores from Excel/GSheets functions:

• Net Present Value (NPV) : KNIME, Excel, Google Sheets,
• Extended Net Present Value (XNPV) : KNIME, Excel, Google Sheets
• Internal Rate of Return (IRR) : KNIME, Excel, Google Sheets
• Modified Internal Rate of Return (MIRR): KNIME, Excel, Google Sheets
• Extended Internal Rate of Return (XIRR): KNIME, Excel, Google Sheets

We created a list of cash flows in excel and computed the different formulas on them.

Then we imported the Excel file in KNIME and run on the same numbers the components.

We were able to achieve the same results of Microsoft Excel within an epsilon of 0.01 in all cases except for XIRR with more than one negative cashflow.

Those are for example 2 portfolios of cashflows with more than 1 negative value:

As you can see there are more than one negative investment (besides the first one) and this gives issue to the implementation by GitHub - RayDeCampo/java-xirr: Java implementation of xirr with bonus Newton-Raphson implementation

For IRR we did not get into any problems within that epsilon and we adopted instead the libary by: GitHub - apache/poi: Mirror of Apache POI

Please keep in mind the goal of this project was not to re-implement the algorithm for this problem, neither to come up with a totally new algorithm.

We simply looked for the most popular open source library to integrate with. We also aimed at giving little problems to KNIME users to adopt the components without additional installations (no Python/R/Conda installation required as both libraries is implemented in Java).

We tried to look at the mathematical problem at first but we realized these algorithms are more or less approximating results by converging to an optimum: that is why they can take more or less time and converge differently as any optimization problem can return different rsults with different algorithm or initialization.

We could not find any information on what Google or Microsoft use in their proprietary version.

If you have questions on the algorithms please reach out to authors of these libraries on GitHub.

Maybe a quick way to solve this would be creating an additional components that take as input the cashflows and the computed IRR or XIRR and computes how close is to the solution (basically a loss function). This way we could have a way to benchmark Excel, Google Sheets, Java libraries and your custom workflow solutions.