k_Means optimization by Silhouette Coefficient

[rogerius1st]

Dear Knimers,
I am currently facing (another) issue with k-Means optimization with Silhouette Coefficient.
I have the following file:
Art_I_clustering.csv (462.8 KB)
I tried to use the suggested component for k-Means optimization: (Optimized K-Means (Silhouette Coefficient) – KNIME Community Hub)
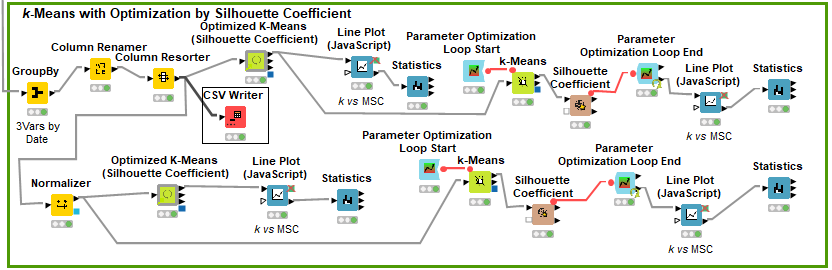
Besides, I also tried (in a parallel comparison), to apply a simplified version of loop for optimizations, with and without normalization. I wished to test the accuracies of such schemes. This way, I got four (parallel) k-Means algorithmic clusterizations, as in the following screenshot (at the left, using the component without (above) and with (below) previous normalization; and the simplified version of loops for optimization, once again, without (above) and with (below) previous normalization:

Finally, my question is:
I got four graphs, and the recomended k number is:
a) for both the non-normalized component AND the simplified loops, the k was 6;
b) for both the normalized component AND the simplified loops, the k was 5.
Both graphs were remarkably different one another, as if they were depicting different realities. Those graphs are in the following (*.DOCX) file:
Graphs for k-Means optimization using component or simplified loops with or without normalization.docx (201.0 KB)
I ask for someone help me to understand – and to explain such difference, because I am drafting a paper whose goal can be better achieved (accessorily) using one clusering technique.
If any other Knime Community member could help me to choose the most correct option and to present a better argument to explain the differences, I would be most grateful.
Best regards.
Rogério.

[gonhaddock]

Hello @rogerius1st
Looking at these charts in .docx that you shared, it’s hard to deliver some conclusions. Even I would say -unknowing the context-, that these chart views aren’t really standard, thinking about an outstanding paper.

I don’t know if you are familiarized with Py coding. Then, I would try to script it, aiming to get some standard charts and silhouette rates for your paper. The chart appearance and rating I’m suggesting should look like this (targeting to be more interpretable):

You would be able to find Py templates in the following topic. This example in the picture is submitted together with the ones from other JKI colleagues:

Solutions to "Just KNIME It!" Challenge 02 - Season 2

A new challenge just came out, folks! This week we’re exploring a topic that we didn’t give much attention to in the past: clustering! This very powerful, unsupervised type of learning should be used this week to segment customers into groups with similar patterns. Here is the challenge. Let’s use this thread to post our solutions to it, which should be uploaded to your public KNIME Hub spaces with tag JKISeason2-2. Need help with tags? To add tag …

BR